Equilibrium of a Co-linear Force System
An object subjected to a force system is in equilibrium if no external effects occur when the force system acts on the object. To be in equilibrium, an object must not move in any direction and must not rotate around any point. Therefore, when the object is in force equilibrium, it must meet the following requirements:
① The algebraic sum of the components of a force system in any direction should be equal to zero
② The algebraic sum of the torque of the forces in the force system with respect to any point (or axis) should be equal to zero.
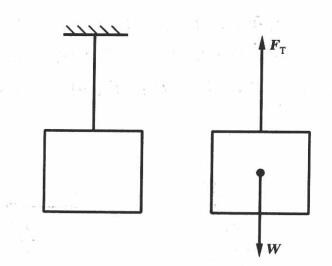
The simplest state of equilibrium is the balance of an object under the action of two forces. According to the law of balance of two forces, if two forces to make the object balance, the two forces must be equal in size and opposite direction, and act in the same line, as shown in Figure 1. The equilibrium equation is
∑ F = 0
And the algebraic sum of the torque at any point A outside the line of action of each force on the force is equal to zero, i.e
∑MA(F)=0
Satisfying either of the above two equilibrium equations will ensure the balance of the system of forces. Obviously, this equilibrium condition can be extended to the equilibrium of the object under the action of any force in the collinear force system, so there is only one independent equilibrium equation for the equilibrium of the collinear force system.


 Mechanics
Mechanics
Comments are closed